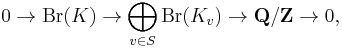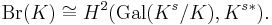Brauer group

In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is named after the algebraist Richard Brauer. More generally, the Brauer group of a scheme is defined in terms of Azumaya algebras.

1 Construction
2 Examples
3 Brauer group and class field theory
4 General theory
5 See also
6 References
7 External links

Construction

A central simple algebra (CSA) over a field K is a finite-dimensional associative K-algebra A, which is a simple ring, and for which the center is exactly K. Note that CSAs are in general not division algebras, though CSAs can be used to classify division algebras.

For example, the complex numbers C form a CSA over themselves, but not over R (the center is C itself, hence too large to be CSA over R). The finite-dimensional division algebras with center R (that means the dimension over R is finite) are the real numbers and the quaternions by a theorem of Frobenius, while any matrix ring over the reals or quaternions – M(n,R) or M(n,H) – is a CSA over the reals, but not a division algebra (if 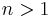$n > 1$ ).

Given central simple algebras A and B, one can look at the their tensor product A ⊗ B as a K-algebra (see tensor product of R-algebras). It turns out that this is always central simple. A slick way to see this is to use a characterisation: a central simple algebra over K is a K-algebra that becomes a matrix ring when we extend the field of scalars to an algebraic closure of K.

Given this closure property for CSAs, they form a monoid under tensor product. To get a group, apply the Artin–Wedderburn theorem (Wedderburn's part, in fact), to express any CSA as a M(n,D) for some division algebra D. If we look just at D, rather than the value of n, the monoid becomes a group. That is, if we impose an equivalence relation identifying M(m,D) with M(n,D) for all integers m and n at least 1, we get an equivalence relation; and the equivalence classes are all invertible: the inverse class to that of an algebra A is the one containing the opposite algebra A^op (the opposite ring with the same action by K since the image of K → A is in the center of A). In other words, for a CSA A we have A ⊗ A^op = M(n²,K), where n is the degree of A over K. (This provides a substantial reason for caring about the notion of an opposite algebra: it provides the inverse in the Brauer group.)

Examples

In the following cases, every finite-dimensional central division algebra over a field K is K itself, so that the Brauer group Br(K) is trivial:

K is an algebraically closed field;

K is a finite field (Wedderburn's theorem);

K is the function field of an algebraic curve over an algebraically closed field (Tsen's theorem).

The Brauer group Br(R) of the field R of real numbers is the cyclic group of order two. There are just two non-isomorphic real division algebras with center R: the algebra R itself and the quaternion algebra H. Since H ⊗ H ≅ M(4,R), the class of H has order two in the Brauer group.

Brauer group and class field theory

The notion of Brauer group plays an important role in the modern formulation of the class field theory. If K_v is a non-archimedean local field, there is a canonical isomorphism inv_v: Br(K_v) → Q/Z constructed in local class field theory. An element of the Brauer group of order n can be represented by a cyclic division algebra of dimension n².

The case of a global field K is addressed by the global class field theory. If D is a central simple algebra over K and v is a valuation then D ⊗ K_v is a central simple algebra over K_v, the local completion of K at v. This defines a homomorphism from the Brauer group of K into the Brauer group of K_v. A given central simple algebra D splits for all but finitely many v, so that the image of D under almost all such homomorphisms is 0. The Brauer group Br(K) fits into an exact sequence

$0\rightarrow \textrm{Br}(K)\rightarrow \bigoplus_{v\in S} \textrm{Br}(K_v)\rightarrow \mathbf{Q}/\mathbf{Z} \rightarrow 0,$

where S is the set of all valuations of K and the right arrow is the direct sum of the local invariants and the Brauer group of the real numbers is identified with (1/2)Z/Z. The injectivity of the left arrow is the content of the Albert–Brauer–Hasse–Noether theorem. Exactness in the middle term is a deep fact from the global class field theory. The group Q/Z on the right may be interpreted as the "Brauer group" of the class formation of idele classes associated to K.

General theory

For an arbitrary field K, the Brauer group may be expressed in terms of Galois cohomology as follows:

$\textrm{Br}(K) \cong H^2(\textrm{Gal} (K^s/K), {K^s}^*).$

Here, K^s is the separable closure of K, which coincides with the algebraic closure when K is a perfect field.

A generalisation of the Brauer group to the case of commutative rings by M. Auslander and O. Goldman, and more generally to schemes, was introduced by Alexander Grothendieck. In their approach, central simple algebras over a field are replaced with Azumaya algebras.

References

V.A. Iskovskikh (2001), "Brauer group of a field k", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=B/b017610

Richard Pierce, Associative algebras. Graduate Texts in Mathematics, 88. Studies in the History of Modern Science, 9. Springer-Verlag, New York-Berlin, 1982 ISBN 0-387-90693-2

Brauer group

Contents

Construction

Examples

Brauer group and class field theory

General theory

See also

References

External links